Snow at above freezing temperatures

From the figure below, it is apparent that there is a clear dependency on the humidity - the drier it is, the warmer can it be while snowing. This implies that the main factor, at least in dry conditions, has to do with humidity. And this factor is evaporation. More specifically, as the snowflakes descend, they evaporate. This process takes heat and keeps the flakes cold.
Thus, if we wish to calculate the maximum temperature, we need to estimate to net heat balance of the flake. First, as the flakes travel in a warm environment, they gain heat from the surrounding through conduction. Second, heat is used to evaporate the flakes, thereby cooling them. If the evaporation heat "sink" is larger than the heat conduction, the flakes will remain frozen.
It turns out that this can be easily calculated. No, it is not simple to calculate the heat conduction or the evaporation heat, but the ratio is, since various unknown geometrical factors cancel out.
If you don't care about the calculation (because you're not a science freak), you can simply visit the calculator page.
If you do care, here is the derivation. Suppose the flow around the flakes is such that a boundary layer of width d forms around it. The total heat flow $F_H$ to the flake (e.g., J/sec in MKS) will be given by Fourier's law:
$$ F_H \approx {\kappa \over c} A {\Delta T \over d}, $$
where $\kappa$ is the heat diffusion coefficient of air (e.g., m²/sec in MKS), c is the heat capacity of air (J/kg in MKS), A is the surface area of the boundary layer around the flake, while ΔT is the temperature difference between the flake and the environment. Similarly, one can use Fick's law to obtain the diffusion of water vapor from the flake (where the temperature is near freezing, and the relative humidity is 100%), to the surrounding environment, where the temperature is higher and the relative humidity lower:
$$ \Phi_W \approx D A {\Delta \rho_W \over d}. $$
Here, D is the water diffusion coefficient
(e.g., m²/sec in MKS) and ρ is the water vapor density (kg/m3 in MKS). The evaporating ice requires heat, thus, if there is a water vapor mass flux of Φ from the flake, it would require heat at a rate of $F_w = \epsilon \Phi$ where $\epsilon$ is the heat of vaporization of ice (J/kg in MKS).
The highest temperature above which the snowflake melts, is the temperature for which the two heat flows are the equal:
$$ F_w = F_H ~~\rightarrow ~~ \epsilon D \Delta {\rho_w \over d} A = {\kappa A \over c} {\Delta T_{max} \over d}.$$
Note that the geometry of the flow around the flake cancels out, because both heat fluxes depend on d and A in the same way. This would be the case also if the boundary layer around the flake is complex such that d actually depends on the direction. Hence,
$$ \Delta T_{max} = c \epsilon {D \over \kappa} \Delta \rho =
c \epsilon {D \over \kappa} \Delta (\rho_{sat} RH).
$$
where $\rho_{sat}$ is the saturation water vapor density.Plugging in the numbers (which can be found for example in the CRC handbook of chemistry and physics), results with an implicit equation for the temperature because the saturation water vapor density depends on the temperature as well. We can simplify things if we instead ask what is the relative humidity required to keep the flake frozen at a given temperature. It is:
$$ RH = 9.5 \exp \left(- 17.27 T_C \over T_C + 238.3^\circ \right) \left( 10.5^\circ\mathrm{C} - T_C\right) \% .
$$
where $T_C$ is the temperature in degree Celsius. This function can be seen in the figure below, together with data from Matsuo and Sasyo, 1981. As can be seen from the figure, the calculated graph is roughly the lower limit below which there is no rain whatsoever. At warmer temperatures, there is a mix. Up to about 1°C above the no melting line, there is mostly snow whereas between about 1°C and 2°C above the line, it is mostly rain, but snow is possible. These events could be due to additional effects, such as strong downdrafts, time it takes to melt the snow, etc.
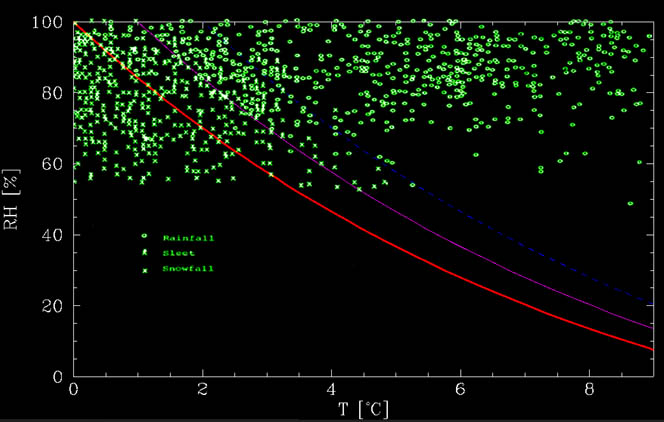
Snow or rain? The red line is the no-melting line. Below it, snow flakes cool by evaporation more than they heat from the environment, thereby keeping themselves frozen. The magneta and blue lines are +1°C and +2°C above the no melting lines. Between 0°C and +1°C above the no melt line, it mostly snows whereas it mostly rains between +1°C and +2°C above the no melt line. At warmer temperatures, it rains. The green data points are events collected by Matsuo and Sasyo (1981) in Wajima Japan, between 1975 and 1978.
Another requirement is that nowhere along the descend does the air surpass the no melt line. If it does, the flake will of course melt.
If the temperature does rise above freezing, there is there are no parameters with which the type of precipitation can be determined for certainty. All that we can then predict is the probability that snow will actually fall. This can be done using the results of Häggmark and Ivarsson (1997), only corrected to use the frozen-bulb and not the wet-bulb temperature.
The bottom line is a calculator with which the probability of snow can be estimated.
How is it related to Wet bulb temperature?
The relationship between the temperature we find and the freezing temperature of water is very similar to the relationship between dry bulb and web bulb temperatures (where the latter is the reduced temperature a wet thermometer will read because of water evaporation). The main difference is that wet bulb temperature includes evaporation of water, whereas in our case, it is evaporation of ice, with 15% more energy loss. Thus, we are essentially looking for the dry bulb temperature for which the "frozen" bulb temperature is 0°C.
References
- Matsuo, T., Sasyo, Y.: 1981, ‘Non-Melting Phenomena of Snowflakes Observed in Sub saturated Air below Freezing Level’, Journal of the Meteorological Society of Japan. 59, 26-32.
- Häggmark, L., Ivarsson, K-I.: 1997, ’MESAN Mesoskalig analys’, SMHI RMK Nr. 75, 21-28.

Comments (12)
This is interesting.
I read somewhere that a much simpler 'rule of thumb' would be to take the average between the air temperature and the dew point. It will snow even if the air temperature is above freezing as long as that average is at freezing or below.
Any comments on this?
This rule of thumb roughly traces the red line in the above graph, but not exactly. So it is in fact a very useful rule of thumb when you don't have a calculator to calculate the "frozen bulb" temperature. Good to know.
The average between the air temperature and dew point is a rough approximation of wet bulb temperature, which lies between these two temperatures.
You lost the epsilon term between the 3rd and the 4th equation. It's not one of the terms that cancel. I'm guessing this is a typo, and that the later equations are correct.
Your argument that F_w=F_H assumes sufficient time for a thermodynamic equilibrium to be established, and for the flake to start melting. How good an approximation is this?
As a side note, the latent heats also change a little bit with temperature, and to a much lesser extent with pressure. Would this have any significant effect on the final result?
I've heard that on rare occasions, it could snow even if the air temperature is 50*F or about 10*C, but usually not more than that. The warmest I've ever seen it snow, if I recall, I think the temperature was 46*F or 47*F with light snow flurries that melted when they came in contact with the ground. Question: is it possible for it to snow in very warm temperatures, like hail does with thunderstorms? Hail is ice, so I was wondering if it can snow at warm temperatures...say, 70*F or 80*F. They say usually, the temperatures should be 30*F to 40*F for snow, but if hail can fall in the summer time with severe thunderstorms, why can't snow?
Hail can fall in the summertime with severe thunderstorms because the ice falls very fast...too fast for the surrounding air teperatures to melt it as it passes through several layers of different temperatures. As snow passes through several layers of different temperatures, it melts as it arrives to "ground temperature".
Hail is much different than snow. For it to snow at more than 46-47 degrees (8-9 C), the conditions would have to be perfect. Hail only occurs because temperatures are cold up higher in the atmosphere (decreasing at 8 degrees every 1000 feet higher). Raindrops freeze at 10-30 thousand feet, and updrafts of heat from ground levels keep them from falling. They collect more rain water, and when the hailstones get high enough, the water freezes on to them and they enlarge. That why hail only appears in strong thunderstorms and on hot days. The hotter it is at ground level, the stronger the updrafts of heat are, and the larger the hailstones can become before they get too heavy for the updrafts to support. In contrast, weak thunderstorms can support freezing raindrops, but there are not enough updrafts to keep them aloft long enough to enlarge. The small bits of ice fall, and melt in the warm ground level temperatures. With snow, the clouds are not high enough to have raindrops freeze into ice. The precipitation starts as tiny ice crystals, and those enlarge into flakes. The ground temperatures, though, are cold enough that no rain falls, but only snow. Anywhere above 50 degrees, and the ground level temperatures melt the snow into rain before it can be seen.
Could it be possible that the snow finally gets converted to rain while coming down to earth? I meant whether snow and rain could simultaneously coexist? If yes, how?
Dr. Shaviv,
I recall this being in the news from several years ago. It is referenced here at RealClimate, but I cannot find anything on this subject. It was quite a big deal back then because the NASA scientist stated the consensus view violated 2LOT.
http://www.realclimate.org/index.php/archives/2004/12/a-statistical-analysis-of-the-consensus/
See the last entry by George E. Smith.
“upset 60 years of climate science”
but will look into it.
Can somebody please simplify this explanation? I'm no dumb ass. I just need a quick answer to my question, "Why do snow and ice melt slowly in the spring even when the temperature is well above freezing?".
Thanks!
First, they are white. As a consequence they absorb less of the sunlight. Second, snow (and not ice) has a lot of small air pockets. This keeps the heat conductivity very low. If you take a look here: http://en.wikipedia.org/wiki/Building_insulation_materials you'll see that all the good insulating materials have air in them.