Estimating the Dipole Radiation Power using Dimensional Analysis
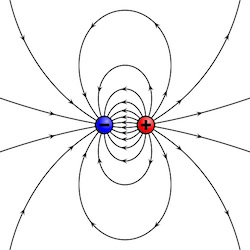
An electric dipole is characterized by the dipole moment $d$ which depends on both the charge $e$ and a the separation $s$ (but not independently on each).
Let us assume we have a dipole oscillating with frequency $\omega$. The relevant equations to describe the problem are obviously Maxwell's equations. Thus, unlike the electrostatic description of the Hydrogen Atom, the speed of light $c$ will be relevant for the solution. Moreover, instead of an expression that depends on the electron charge $e$, we will seek one which depends on the dipole moment $d$, which is charge times displacement: $\left[d\right] = esu \cdot cm$. The expression will obviously depend on $\omega$ as well. It wont depend on $\hbar$ because the problem is not a quantum mechanical one. Likewise, the expression will also be independent of $G$ because the problems is unrelated to gravity.


