general physics

Estimating the power radiated by an oscillating electric dipole is an excellent example for the usage of dimensional analysis.

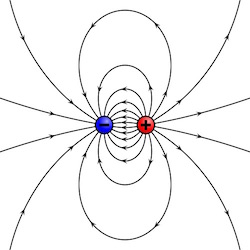
Let us assume we have a dipole oscillating with frequency $\omega$. The relevant equations to describe the problem are obviously Maxwell's equations. Thus, unlike the electrostatic description of the Hydrogen Atom, the speed of light $c$ will be relevant for the solution. Moreover, instead of an expression that depends on the electron charge $e$, we will seek one which depends on the dipole moment $d$, which is charge times displacement: $\left[d\right] = esu \cdot cm$. The expression will obviously depend on $\omega$ as well. It wont depend on $\hbar$ because the problem is not a quantum mechanical one. Likewise, the expression will also be independent of $G$ because the problems is unrelated to gravity.

An LC circuit is one which has a capacitor and an inductor connected to each other. It exhibits oscillations just like a mass on a spring (a harmonic oscillator). In fact, the analogy is quite accurate with the capacitor playing the role of the spring and the inductor playing the role of the mass inertia.

Just like any harmonic oscillator, we can use equipartition to estimate the energy and frequency of oscillations using equipartition.

The average energy in the capacitor is: $$

Ever wondered whether it was sufficiently cold for sufficiently long to allow you to stand on ice, without falling in? I once did. Here is an estimate for the duration required to reach a given thickness. Actually, it is a lower limit, since we assume a few simplifying assumptions.

Many physical systems have a tendency to equilibrate the energy between different subcomponents. Sometimes it is exact, and sometimes not. For example, in an acoustic wave, the wave's energy is on average half kinetic (motion of the gas) and half internal (pressure). In the interstellar medium, there is roughly the same energy in the different components, such as internal energy, turbulent energy, magnetic field and energy of the cosmic rays. Stars are no different. In the sun, there is roughly the same binding energy (which is negative) as there is thermal energy. This can also be shown using the virial theorem. In white dwarfs, the thermal energy is unimportant, instead, there the degenergy energy of the electrons is comparable to the binding energy. We can use this tendency for equipartition to estimate different stellar parameters.