Bush in a quantum entangled state
Nope, it isn't a science driven blog entry (though given that it is a science blog, I will include one calculation for fun and even an analogy to quantum entanglement, hence the title). The trigger for this entry was the fact that I preferred working at home than going to work and getting stuck in traffic jams caused by President Bush's visit to my humble town of Jerusalem, so instead of suffering from it, I decided to write about it. It's called beating around the Bush.
Living here in Jerusalem is actually quite interesting, the city has a very rich history (well, as rich as it gets), varied geography (mediterranean forested hills on one side, desert on the other), interesting population (e.g., our semi-detached neighbor is an ambassador) and close to perfect climate (at least from my point of view). As the capital of an interesting country, it also gets many interesting visitors. In fact, on the evening before yesterday, my astrophysics group had the honor of hosting Prof. Scott Tremaine (very interesting by himself). We went to a fancy Moroccan restaurant, and sitting a few paces away were non other than Tony Blair and the Israeli foreign minister Tsipi Livni. This is not unusual in this city.
Anyway, I was happily working at home yesterday at the Jerusalem suburb of Mevasseret Zion, as the sky above me turned into a helicopter highway (literally). Overhead passed quite a few helicopters, some Israeli and some American. At some point, however, the rumbling obtained a lower pitch, so I realized it was the Bush convoy with the two heavy CH-46 Sea Knight helicopters (someone told me it was CH-47 Chinooks, but I am mostly certain they were not) and two seahawks. Below is a picture of them approaching Jerusalem.

Bush's convoy above Mevasseret Zion, 10 km west of Jerusalem. Apparent are two sea knight helicopters.
Today I dared entering Jerusalem and going to the office. The noise was really bad. It turns out that the university's soccer and track field, a few hundred meters away from my office was turned into a busy heliport, and surrounding it (including the roof of my building) were quite a few Israeli border policemen. A few will pop up again in this story.

A view from my office. A sea knight taking off. The Knesset (Israeli parliament) is in the background

Two seahawks above campus (the two buildings are Ross [computer science, left] and Kaplun [physics, right]). To some extent, Bush is in these helicopters...
At some point, bush came with a 4 helicopter convoy (he returned from his visit to the church of the nativity in Beth-Lehem), which included two Sea Knights and two Seahawks. A friend ask me in which one of them was George W. Bush. I told her that he could be in any. They rotate to make sure nobody knows (at least I don't!). At that point I realized that it is almost as if Bush was in a quantum entangled state. When flying from Ben-Gurion airport to Jerusalem for example, he was flying a seahawk (he was seen entering one...), so his state was a combination of both helicopters at equal probability. If his presence in seahawk A can be described by the two states basis of $\{\left|0\right\rangle_A, \left|1\right\rangle_A\}$, while his state in seahawk B can be described by the two states $\{\left|0\right\rangle_B, \left|1\right\rangle_B\}$, then we can say that Bush was prepared in the following entangled state:
$${1\over \sqrt{2}}\left( \left|1\right\rangle_A \otimes \left|0\right\rangle_B - \left|0\right\rangle_A \otimes \left|1\right\rangle_B \right).$$
Once anyone "measures" Bush in to be in one particular helicopter, immediately his quantum state will collapse to $\left|1\right\rangle$ in that helicopter, while his state in the second seahawk will collapse to $\left|0\right\rangle$. This is probably one entanglement Bush didn't think of...
Little did I know, I almost got entangled myself with the local law. As I went to my parked car (I had to leave, to pick up my kid from daycare) I glimpsed towards the nearby track field and realized that through the woods I could see a quarter of Bush (well, the whole of his chopper with some 1/4 probability to be exact...), so I decided to capture a few photons on my iphone camera. A few milliseconds later, a normal police van stopped behind me asking me what I was doing. They politely (I'm being cynical here) offered me to tow my car away for being prudent. I dared them, since I wasn't doing anything illegal. (Actually, I wished I'd dared... I just went to the car like a nice citizen would do).

The secluded landing site for his majesty (well, they treated him like a king) George W. Bush at the Hebrew University
O.k., enough of the story. Here is a small physics calculation.
Can one estimate the maximum possible speed of the Sea Knight helicopters?
The answer is of course positive. To make it interesting though, I'll use the audio from the video I captured of the sea knights (the top figure above is a video capture).
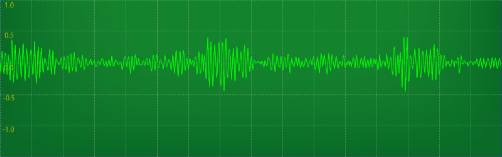
Audio waveform of 2 sea knights and one seahawk, though it is the sound of one sea knight which is dominating. Each horizontal division is 10 ms, hence, the rotors flap with a period of 60ms. (16.7 Hz)
In principle, one could measure the diameter of the sea knight's blade from the second image above (it requires knowing the distance between my office and the track field plus some simple trigonometry. Since I'm lazy, I'll just google for it (I could also google for the maximum speed but that would beat the point, wouldn't it?). The diameter is 16 meters.
From the audio waveform above, it is evident that the vibration period of the 3 bladed rotors is 1/0.06=16.7 Hz. Thus, the speed of the tips of the blades, relative to the helicopter are $$v_{rel} = \pi \times 16m\times 16.7 (1/sec) /3 = 279 m/s.$$
The main point to note about helicopter blades is that they are not supposed to pass the speed of sound. Once they do, the shock waves excite horrible vibrations in the blades, cause too much metal fatigue and many other problems. Thus, we know that the speed of the helicopter plus the speed of the blades cannot surpass the speed of sound. This implies that the maximum speed of the chopper has to satisfy $v_{max} \lesssim v_{s} - v_{res}$. Taking the standard speed of sound at 15°C, we find: $$v_{max} \lesssim 340m/s-279m/s = 61m/s = 220 km/hr.$$
According to the all knowing google, the maximum speed of the Sea Knight is supposed to be 265 km/hr, somewhat higher than our estimate... but not far off it either!

Comments (9)
Wow shaviv, I don't know much (if any) physics, let alone wave physics, this piece is still a reason for applauds
Physics was never my forte - however when it comes Bush - well I guess physics was never his forte either
"will include one calculation for fun"
Unless I'm misunderstanding the nature of the first set of expressions, there are two. Also, I think you forgot to capitalize Bush a couple of times. Don't shoot.
Interesting info, both on Jerusalem and Helicopter's max speed calculations. And Bush in a quantum entangled state. Sort of an odd combination.
1) Well... I wouldn't call the first set of equations a calculation, but perhaps it sort of is.
2) Yep, I didn't capitalize him a few times. Perhaps it was intentional... perhaps (more likely) it wasn't.
3) Odd science bits... that's the essence here!
Actually according to wikipedia the maximum speed of the sea knight is 265km/hr. The seahawk is a bit faster, but those pictures do seem more like a sea knight. At least some of the difference can be attributes to the fact the blades are at an angle of attack with respect to the direction of motion thus you need not add all of their speed to the helicopter speed. However to counter that, the supersonic effects of the blade happen before the blade reaches the speed of sound as the blade causes the air to travel faster over it's top.
As for the maximum speed, I never realized that helicopters are more sensitive to the temperature outside: The higher the temperature, the higher the speed of sound and the faster can the helicopters go. However, unlike planes, because the helicopters' top speed is determined by the difference between the blade speed and the speed of sound, the relative change can be more important.
Thus, if we're talking about 30°C instead of 15°C, the speed of sound should increase by a factor of $\sqrt{(273+30)/(273+15) = 1.052$, i.e., just over 5%. However, it can increase the maximum speed of the helicopter by 63 km/hr, which is not negligible at all compared with the typical speeds of 250 km/hr. Thus, it could be that the maximum rated speed is under favorable conditions, i.e., a high temperature.
– Nir
p.s., didn't realize that you read my blog...
p.s., didn't realize that you read my blog...
First time I did...
Still think you are neglecting the angle of attack.
Using the info on sea knights on wikipedia (and in particular, the drawings of it), one can learn that the rotors have a width of about 40cm. Thus, their total surface area is $A = 0.40m \times 8m \times 3 \approx 10 m^2$ (since their length is 8m each, and there are 3 of them).
Next, we know from bernoulli that the pressure difference between the top and bottom is $\Delta p = (1/2) \rho_{air} (v_{top}^2 - v_{bottom}^2) \approx \rho_{air} v \Delta v$.
Next, this pressure difference should hold the $m=10$ ton helicopter. That is, $$ A\Delta p = m g ~~\rightarrow~~ \Delta v \approx {m g \over A \rho_{air} v} \approx {10^4 kg~10~m/sec^2 \over 10~m^2~1.2~ kg/m^3~ 250~m/sec} \approx 33~ m/sec$$ Of course, we have to realize that if this is the velocity difference, then the velocity on top is the average plus half of it. On the other hand, there is probably a range of velocities given that the blade is moving at a different speed at different radii.
So, bottom line, the angle of attack is typically a 10% correction.
Knight indeed
http://www.globalsecurity.org/military/systems/aircraft/ch-467.htm