Passing the Eddington limit without getting a ticket
Nir J. Shaviv
We review here the theory of porous atmospheres and how super-Eddington systems can arise. Before we actually do so, we begin with a background to remind us of the Eddington luminosity limit and the standard lore, that there is a maximum luminosity with which objects can shine in steady state. The background also summarizes the main observational evidence demonstrating the existence of super-Eddington objects, that is, that the standard lore is in fact wrong.
Radiation exerts a pressure. This implies that in luminous systems there is an outwards force by the outgoing luminosity, in addition to the gravitational force pulling the gas inwards. In the sun, this radiative force is more than 10,000 times smaller than the gravitational pull, but in more massive stars, this outward radiative force can approach the force of gravity.
Under the classical picture, one cannot surpass the Eddington limit while keeping the system in steady state, because nothing could balance the net force outwards, and gas will necessarily be accelerated outwards, thereby "evaporating" the system. In a supernova explosion, for example, the large fluxes accelerate gas outwards and the systems are quite far from a steady state, so the limit does not apply. But in systems which remain intact for durations much longer than their dynamical time scale, the limit should be relevant, at least according to the classical picture.
Since the radiative flux and gravitational force both fall like the distance from the center of the object squared, the critical luminosity above which no steady state should exist does not depend on the distance from the center of the object, just the the total mass for the object. This critical luminosity, called the Eddington luminosity, is:
Described above is the succinct argument why a maximum luminosity should exist. There are however several systems in nature where super-Eddington behavior is unequivocally observed. Other systems may surely exist, but it is more complicated to prove their super-Eddington nature and are therefore less convincing.
During the great eruption, the star, which is generally not one of the more conspicuous ones in the sky became the second brightest, second only to Sirius! Given that it's estimated mass is of order 100 solar masses, the high luminosity implies that the star must have been radiating at at least 5 times its Eddington luminosity. At this high luminosity, the object should have shed much more mass than it did, but it ejected "only" a few solar masses of material. Under a standard stellar atmosphere description, no consistent solution can be found.
Of course, if η-Car is a 500 solar mass star, it need not have been super-Eddington, but such a hypothetically massive star would have found it hard to exist given that it would have been terribly unstable. (Such stars, or even more massive ones could have existed as the first generation of stars when heavy elements were absent, but not today in our galaxy).
Since white dwarfs cannot be more massive than the Chandrasekhar limit, an eruption brighter than 100000 Lsun is necessarily super-Eddington irrespective of the actual mass of the white dwarf or the actual hydrogen content in the atmosphere, (i.e., the Eddington limit is expected to be generally even smaller).
The brightest novae can reach much brighter luminosities. For example, Nova LMC 1991 reached a staggering 700000 Lsun, and was therefore super-Eddington for at least 2 weeks. Clearly, novae unequivocally prove that objects can shine brighter than their Eddington luminosities for durations longer than their dynamical time scale by orders of magnitude. Novae may have fallen out of the top list of sexy astrophysical objects, but they are nonetheless one of the best super-Eddington object to study. This is especially the case considering the ample observational data that exists.
From theory we do not expect objects to surpass the Eddington limit, evidently however, nature finds a way to surpass the limit. Below I describe the only theory which explains how such steady state systems can surpass the Eddington limit. The main merit of the theory is that it correctly predicts various observed characteristics of these systems, in particular, the winds that these objects accelerate.
Before getting into details, let us begin with the big picture, which explains how atmospheres can surpass the Eddington limit. Namely, how atmospheres can have a very high flux without blowing themselves apart:
(a) The inner parts: When an object, like η-Car, becomes super-Eddington, i.e., when the total energy it emits is larger than the Eddington luminosity, most of the object will actually witness a sub-Eddington radiative flux. This is because as the Eddington Luminosity is approached, convection (i.e., the transport of heat using macroscopic flow, such as water in a boiling pot) is always excited, and is efficient enough to keep the bulk of the star sub-Eddington. That is, enough energy transport is taken away from the radiation field, such that the remaining flow is kept below the Eddington luminosity.
(b) A porous atmosphere - The crucial element behind super Eddington atmospheres: Convection requires dense enough gas. When the gas density is not high enough, convection is not efficient and the bulk of the energy flow should be carried by the radiation. The radiative flow should then be super-Eddington. Interestingly, however, the layer remains effectively sub-Eddington. The flux itself is super-Eddington, but the total force exerted by the radiation field is below that expected from a super-Eddington luminosity. How come? The secret is the fact that these atmospheres will become inhomogeneous or porous, such that instead of passing through all the material, the radiation field is funneled through cavities or regions with less mass. That is, the radiation field bypasses the obstacles.
(c) Optically thick wind - When perturbations arising from the instabilities (which are expected to be of order the atmospheric scale height - the length scale over which the density significantly falls), lose their opaqueness, the effective opacity tends to the microscopic value and the effective Eddington limit tends to the classical value. At that radius, the effective Eddington luminosity is equal to the total luminosity. From that point outwards, there is a net force outwards and a wind is accelerated.
(d) Optically thin wind - At a large enough radius, the geometrical dilution makes the wind transparent. The boundary between the regions is the photosphere of the object - i.e., the apparent surface. Namely, it resides in the wind. The static part of the object itself is obscured.
-- continue to page 2 --
We review here the theory of porous atmospheres and how super-Eddington systems can arise. Before we actually do so, we begin with a background to remind us of the Eddington luminosity limit and the standard lore, that there is a maximum luminosity with which objects can shine in steady state. The background also summarizes the main observational evidence demonstrating the existence of super-Eddington objects, that is, that the standard lore is in fact wrong.
1. The Eddington Luminosity:
Sir Arthur S. Eddington
Under the classical picture, one cannot surpass the Eddington limit while keeping the system in steady state, because nothing could balance the net force outwards, and gas will necessarily be accelerated outwards, thereby "evaporating" the system. In a supernova explosion, for example, the large fluxes accelerate gas outwards and the systems are quite far from a steady state, so the limit does not apply. But in systems which remain intact for durations much longer than their dynamical time scale, the limit should be relevant, at least according to the classical picture.
Since the radiative flux and gravitational force both fall like the distance from the center of the object squared, the critical luminosity above which no steady state should exist does not depend on the distance from the center of the object, just the the total mass for the object. This critical luminosity, called the Eddington luminosity, is:
$$ L_{\rm Edd} = {4 \pi G M_\star c \over \kappa_m} \approx {6.6 \times 10^4 \over 1+X}{M\over M_\odot} L_\odot, $$
with $\kappa_m$ being the opacity per unit mass.
What is Opacity? The main parameter determining the interaction between matter and radiation is the Opacity. Basically, it tells how much matter is required to stop a photon on average. It is generally measured in units of amount of mass per unit area. The smallest opacity for ionized material is that of obtained by Thomson scattering, which is scattering by the free electrons. It is roughly 0.2-0.4 cm2/gr. For comparison, earth's atmosphere is about 1000 cm2/gr. The reason the atmosphere is transparent is because the electrons are bound to their parent atoms and thus cannot scatter light (unless it is energetic enough to excite the electrons, which is why the atmosphere is opaque at UV). Under normal stellar conditions, Thomson scattering is the lowest opacity which can be obtained (when the temperatures are high). In porous atmospheres, as we shall see below, the effective opacity is reduced because it is easier for the radiation to escape without exerting as much force on the gas.
2. Nature Surpassing the Eddington Limit
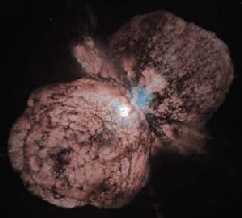
The Homunculus Nebula of η-Car. It was ejected during the 20 year long great eruption in the late 19th century. During the eruption, the object shined at several times its Eddington limit. The nebula's mass is a few solar masses. It may sound huge, but it is in fact much smaller than theoretically expected given that the object was super-Eddington.
a. η-Carina as a super-Eddington object
The star is certainly one of the more interesting objects in our galaxy. It is a very luminous massive star (and possibly a binary). It is also a Luminous Blue Variable, which implies that it erratically changes its luminosity. One such flare up was its 20 year long eruption in the late 19th century.During the great eruption, the star, which is generally not one of the more conspicuous ones in the sky became the second brightest, second only to Sirius! Given that it's estimated mass is of order 100 solar masses, the high luminosity implies that the star must have been radiating at at least 5 times its Eddington luminosity. At this high luminosity, the object should have shed much more mass than it did, but it ejected "only" a few solar masses of material. Under a standard stellar atmosphere description, no consistent solution can be found.
Of course, if η-Car is a 500 solar mass star, it need not have been super-Eddington, but such a hypothetically massive star would have found it hard to exist given that it would have been terribly unstable. (Such stars, or even more massive ones could have existed as the first generation of stars when heavy elements were absent, but not today in our galaxy).
b. Novae as super-Eddington objects:
Novae are white dwarfs which accrete hydrogen rich material from a companion star. Once enough material is accumulated, it undergoes a thermonuclear runaway where the hydrogen is ignited, and burned into helium. Once the system stabilizes, its expected steady state is that given by the Core Mass Luminosity Relation first described by Paczynski in 1970. The luminosity of this steady state is expected to be a function of the core (WD) mass, but not that of the envelope. It should increase with core mass and saturate at the Eddington luminosity limit.Since white dwarfs cannot be more massive than the Chandrasekhar limit, an eruption brighter than 100000 Lsun is necessarily super-Eddington irrespective of the actual mass of the white dwarf or the actual hydrogen content in the atmosphere, (i.e., the Eddington limit is expected to be generally even smaller).
The brightest novae can reach much brighter luminosities. For example, Nova LMC 1991 reached a staggering 700000 Lsun, and was therefore super-Eddington for at least 2 weeks. Clearly, novae unequivocally prove that objects can shine brighter than their Eddington luminosities for durations longer than their dynamical time scale by orders of magnitude. Novae may have fallen out of the top list of sexy astrophysical objects, but they are nonetheless one of the best super-Eddington object to study. This is especially the case considering the ample observational data that exists.
From theory we do not expect objects to surpass the Eddington limit, evidently however, nature finds a way to surpass the limit. Below I describe the only theory which explains how such steady state systems can surpass the Eddington limit. The main merit of the theory is that it correctly predicts various observed characteristics of these systems, in particular, the winds that these objects accelerate.
3. The Big Picture
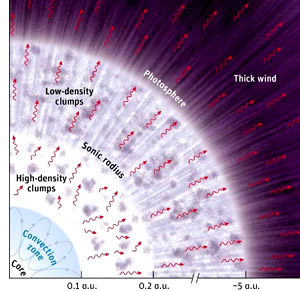
The Structure of η-Car during its great Eruption - The archetype Super-Eddington Object. From the inside out, the star includes: (A) A convective layer, where enough energy is transported by moving gas elements (like boiling water), thereby keeping the radiation low. (B) A porous atmosphere, where the radiation is super-Eddington but since it passes through low density regions between high density clumps, the net radiative force is reduced and the atmosphere remains stable. (C) A wind (above the sonic radius), composed of an optically thick (i.e., opaque) wind but with optically thin "blobs" and (D) an optically thin (transparent) part above the photosphere. More detail in the text. (Diagram from Sky & Telescope article on the topic, based on a diagram by the Author)
(a) The inner parts: When an object, like η-Car, becomes super-Eddington, i.e., when the total energy it emits is larger than the Eddington luminosity, most of the object will actually witness a sub-Eddington radiative flux. This is because as the Eddington Luminosity is approached, convection (i.e., the transport of heat using macroscopic flow, such as water in a boiling pot) is always excited, and is efficient enough to keep the bulk of the star sub-Eddington. That is, enough energy transport is taken away from the radiation field, such that the remaining flow is kept below the Eddington luminosity.
(b) A porous atmosphere - The crucial element behind super Eddington atmospheres: Convection requires dense enough gas. When the gas density is not high enough, convection is not efficient and the bulk of the energy flow should be carried by the radiation. The radiative flow should then be super-Eddington. Interestingly, however, the layer remains effectively sub-Eddington. The flux itself is super-Eddington, but the total force exerted by the radiation field is below that expected from a super-Eddington luminosity. How come? The secret is the fact that these atmospheres will become inhomogeneous or porous, such that instead of passing through all the material, the radiation field is funneled through cavities or regions with less mass. That is, the radiation field bypasses the obstacles.
(c) Optically thick wind - When perturbations arising from the instabilities (which are expected to be of order the atmospheric scale height - the length scale over which the density significantly falls), lose their opaqueness, the effective opacity tends to the microscopic value and the effective Eddington limit tends to the classical value. At that radius, the effective Eddington luminosity is equal to the total luminosity. From that point outwards, there is a net force outwards and a wind is accelerated.
(d) Optically thin wind - At a large enough radius, the geometrical dilution makes the wind transparent. The boundary between the regions is the photosphere of the object - i.e., the apparent surface. Namely, it resides in the wind. The static part of the object itself is obscured.
-- continue to page 2 --