Vacuum QED effects detected around Neutron Stars?
Just over a week ago I received an interesting call from a reporter from science magazine. He asked me what do I think about the recent discovery of the Quantum Electrodynamic (QED) produced vacuum birefringence around neutron stars. It was an interesting surprise as my colleague Jeremey Heyl at the University of British Columbia and I had what seemed to be a bizarre prediction back in around 1998, a prediction which seems to have been verified almost 2 decades later. So, what is the effect and what was measured?
In 1936, Heisenberg, Euler and separately Weisskopf realized that light rays can interact with the virtual electrons in the vacuum if there is a very strong magnetic field. This interaction causes the electrons to oscillate and produce an electromagnetic wave such that the sum is an electromagnetic wave appearing to move slower than the speed of light. This is very similar to what happens with real electrons in everyday media (e.g., in your glasses where light moves slower than the speed of light), except that in everyday situations the interaction is not with the vacuum's virtual electrons.
As a consequence of this interaction, the index of refraction is different from unity. However, the cool thing is that the two indices of refraction of the two polarization states (in the direction perpendicular to the magnetic field and perpendicular to the latter) are different. This is because electrons oscillating in the direction of the magnetic field are not affected by it (well, almost), while electrons oscillation perpendicular to the magnetic field are. Thus, not only is the index of refraction different from unity, it is different for the two polarization models of the light, namely, depending on how the light ray's electric field is oriented with respect to the magnetic field. This effect is called birefringence (and it is wavelength independent for the vacuum birefringence).
In everyday life, birefringence can be seen in different polymeric materials in which the polymers have a preferred direction (e.g., by stretching cellophane). It can also be found in some natural crystals, the common of which is calcite.
To understand what happens, let us look at a light ray that has both polarization states. When the ray passes from vacuum (or similarly air) into the birefringent medium, the two modes are refracted differently and separated into the two polarization states this can be seen in the two images below. Figure 1 shows the different refraction of the two modes, while figure 2 shows how this then gives rise to having the "calcite" text seen twice.
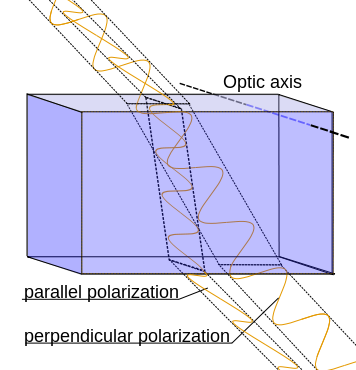
Fig. 1: When a light ray passes from vacuum or air into a birefringent medium, the two polarization modes refract differently. Each one propagates in a different direction.

Fig. 2: Calcite is a natural example of birefringence. Because the two polarization states refract differently, the underlying "calcite" text is seen twice at different directions.
If the original state is linearly polarized in a direction intermediate between the two states, it will therefore be separated into the two polarizations defined by the principle axes of the birefringent medium. Thus, if you have two birefringent media touching each other, but oriented differently, then a light ray that passes from one medium will necessarily split into two rays as it passes into the second medium (since the original polarization in the 1st medium is in a direction different from the separate polarization states in the 2nd medium).
What happens however if there is a gradual change in the primary polarization directions between the two media? It turns out that if the change is sufficiently slow, then the polarization rotates together with the change in the primary axes. This "adiabatic" evolution takes place only if the modes are sufficiently distinct over the typical distance over which the direction of the principle polarization directions change. (In more technical terms, the difference in the polarization mode's wavevectors has to be larger than the inverse of the distance scale for changes in the direction).
For vacuum birefringence around neutron stars, adiabatic evolution means that each polarization state follows the direction of the magnetic field as it propagates away from the star. Moreover, since the birefringence is wavelength independent, but the wavevectors (and therefore their difference) is larger for higher frequencies, adiabatic evolution is more effective at higher frequencies for which the re-coupling of the modes takes place further away. This can be seen in the animation I created back in 1998(!), which required some digging in old hard-disks to be found. The animation was created for radio waves where plasma birefringence is important, i.e., interaction with real electrons. Here the effect is larger for longer wavelengths, as can be seen in the animation.
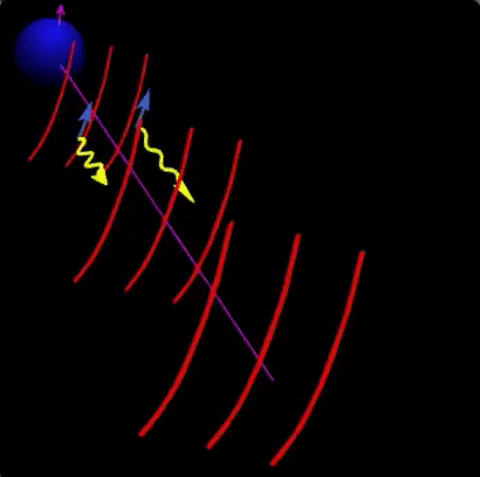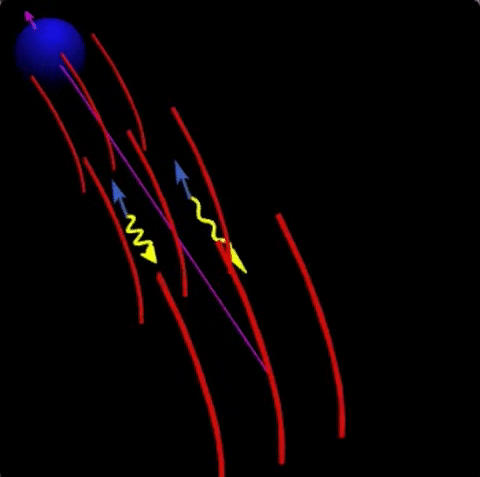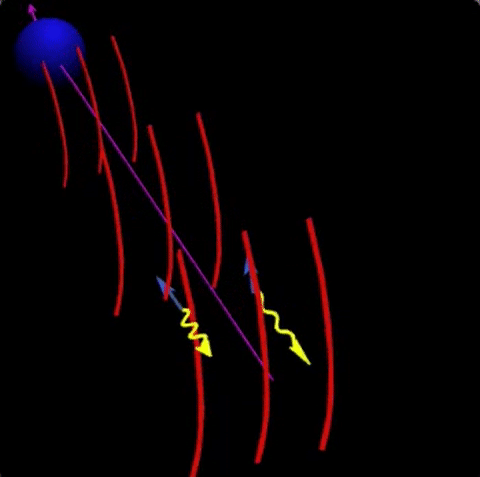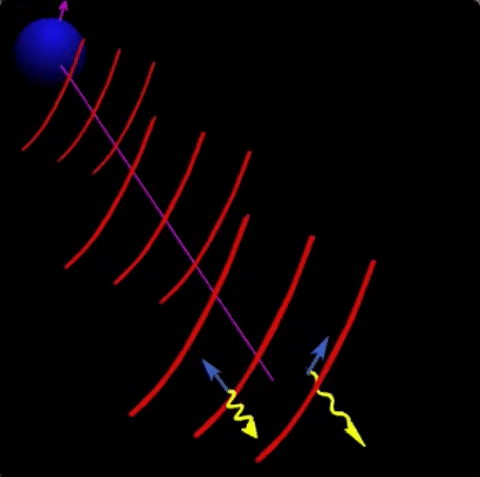
Fig. 3: As electromagnetic ways propagate away from the neutron star, adiabatic evolution arising from birefringence implies that the polarization directions follow the magnetic field. For radio waves, plasma birefringence implies that longer wavelength waves a coupled up to larger distances (as seen in the animation). For optical and shorter wavelengths, vacuum birefringence implies that the effect is opposite, shorter wave are coupled up to larger distances.
This adiabatic evolution has a very interesting effect. The local magnetic field at the surface of the neutron star has a different direction. Therefore, polarized light leaving the surface would be polarized in different directions. The total polarization measured by a distant observer would therefore mostly cancel out. However, the effect of the adiabatic evolution is to let the polarization states follow the direction of the magnetic field. If the recouping of the modes takes place far enough, then the rays coming from different locations of the surface would now add up as the polarization direction would now be very similar for the different light rays. This can be seen in fig. 4.
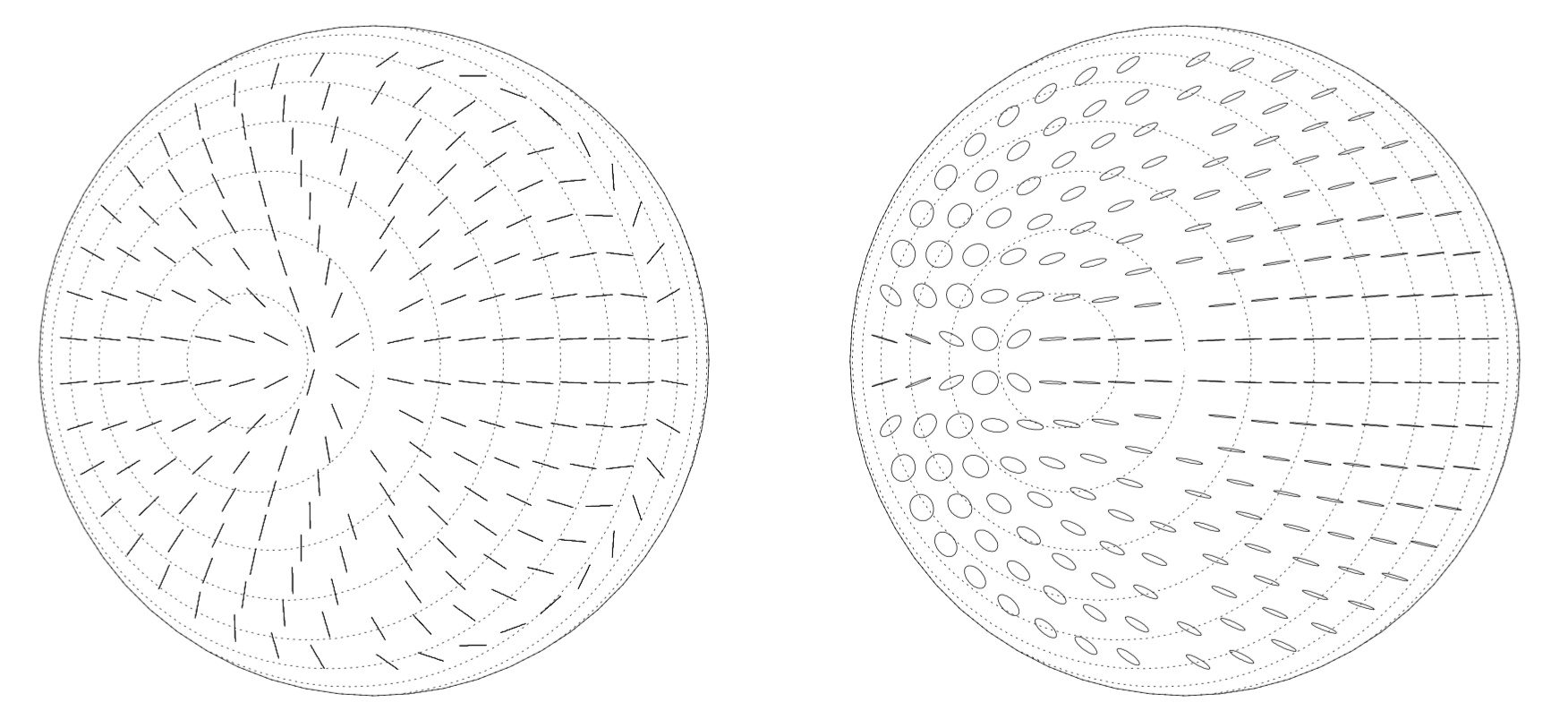
Fig. 4: The direction of the polarization at the surface will depend on the local magnetic field. If adiabatic evolution takes place, then once the rays recouple, the polarization directions will tend to align giving a much large net polarization. Here we have assumed that the light leaving the surface is 100% polarized at a frequency of about 10^17 Hz (and a dipole moment of 10^30 G cm^3). From ref. 2.
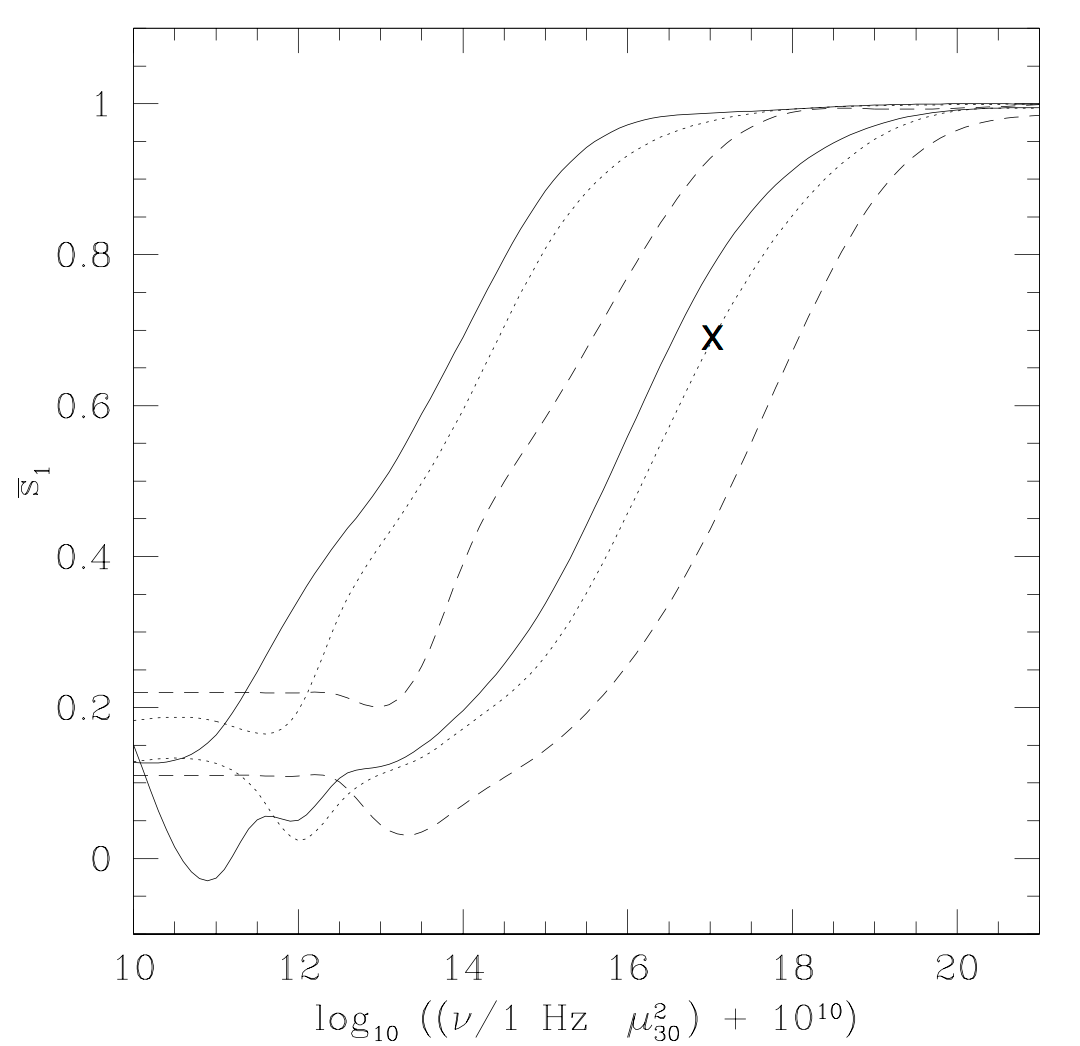
Fig. 5: The net polarization to be observed as a function of frequency for three different NS radii solid line—6 km; dotted line—10 km; dashed line—18 km and two observer magnetic co-latitudes: upper three curves—60° ; lower three curves—30°). The graphs assume that the surface has a uniform temperature and the emissivity is spherically symmetric. The case depicted in the previous figure is marked by an ‘‘X.’’ It should be compared with the low frequency limit of the curve, for which QED is unimportant.
Thus, the prediction that Jeremey Heyl and I made back in a paper published in 2000 (see ref. 1 below) is that thermal radiation coming out from neutron stars will have a much higher polarization than can be expected otherwise. It should be noted that we expect the thermal radiation to be polarized because the transparency of the surface layers is different in the two polarization modes such that it is much easier for one polarization mode to be radiated than it is with the other. However, as mentioned above without adiabatic evolution it would be averaged away.
The recent observation (ref. 3) is a detection in visible light of a relatively large polarization of the thermal radiation emanating from a neutral star that is 400 light years away. It is extremely faint, so it is a very hard measurement to do, but still, the authors (Mignani et al., ref 3) managed to detect the polarization. They have also shown that all the nearby stars are not polarized, implying that it is not a galactic medium effect.
However, even so, they haven't proved that what they have seen is indeed vacuum birefringence and not for example plasma birefringence. At low frequencies, the plasma around a pulsar is birefringent giving rise to similar effects (this time from interaction with real electrons). To prove that, they need to carry out another polarization measurement at a higher frequency and show that it is indeed larger.
Once confirmed, it will show how non-trivial QED effects take place in nature. It will also be used as another tool to study neutron stars and their magnetic fields more directly (than neutron spin down for example). Now you can read the article in science.
References:
1. J. S. Heyl & N. J. Shaviv, Polarization evolution in strong magnetic fields, Monthly Notices of the Royal Astronomical Society, 311, 555 (2000). [The original paper were we discuss the effect of vacuum birefringence on the evolution of the polarization]
2. J. S. Heyl & N. J. Shaviv, QED and the high polarization of the thermal radiation from neutron stars, Phys. Rev. D, 66, 023002 (2002). [The paper were we calculate more realistically the expected polarization from the thermal radiation of neutron stars].
3. González Caniulef et al., Polarized thermal emission from X-ray dim isolated neutron stars: the case of RX J1856.5-3754, Monthly Notices of the Royal Astronomical Society, 459, 3585 (2016). [The recent observational paper describing the detection of high polarization from a neutron star in visible light]
4. A. Cho, Astronomers spot signs of weird quantum distortion in space, Science, Nov 30 (2016). [A short editorial about the detection in science magazine]
